5.3 訂貨批量
5.3.1 確定訂貨批量的方法
確定訂貨批量的目標(biāo)有兩個(gè)方面,即使得所涉及的成本之和最小,使客戶服務(wù)水平最高。
關(guān)于訂貨批量,如今人們的興趣已經(jīng)從經(jīng)濟(jì)訂貨批量(EOQ)的經(jīng)典問(wèn)題轉(zhuǎn)移到離散需求環(huán)境下的訂貨批量問(wèn)題上來(lái)了。這個(gè)變化是由于MRP的出現(xiàn)而引起的。因?yàn)镸RP系統(tǒng)是通過(guò)計(jì)算按時(shí)間分段的總需求量和凈需求量,并以間斷的時(shí)間序列來(lái)表達(dá)對(duì)物料的需求。
常用的確定訂貨批量的方法有如下幾種:固定訂貨批量法、經(jīng)濟(jì)訂貨批量法、按需確定批量法、根據(jù)固定時(shí)區(qū)的需求確定批量法、時(shí)區(qū)訂貨批量法、最小單位費(fèi)用法、最小總費(fèi)用法、Wagner-Whitin法。其中,前兩種方法是面向需求率的,特別是第二種方法,是基于需求連續(xù)、需求率穩(wěn)定這一前提的。這兩種方法都是確定一個(gè)固定的批量,每次都按這個(gè)批量訂貨。其余方法則是所謂間斷批量確定方法。這些方法的訂貨批量是變動(dòng)的,根據(jù)一個(gè)或幾個(gè)后續(xù)計(jì)劃時(shí)區(qū)內(nèi)的凈需求量來(lái)確定批量,使訂貨批量與凈需求量相等,因此,不會(huì)產(chǎn)生剩余物料又不足以滿足下一個(gè)計(jì)劃時(shí)區(qū)的需求的情況。
下面我們分別討論這些確定訂貨批量的方法。
1. 固定訂貨批量法
固定訂貨批量法(fixed order quantity,F(xiàn)OQ)可用于MRP控制下的所有物料,但在實(shí)踐中,通常只限于訂貨費(fèi)用比較大的部分物料。對(duì)這些物料,根據(jù)凈需求量的大小變化而不斷發(fā)出訂貨是不上算的。所以,常采用固定批量的形式訂貨。訂貨的數(shù)量可以根據(jù)經(jīng)驗(yàn)來(lái)決定。
在表5.1中給出了例子。其中,9個(gè)時(shí)區(qū)的凈需求量數(shù)值將沿用于以下對(duì)各種訂貨量方法的討論中。
表5.1 固定訂貨批量法
2. 經(jīng)濟(jì)訂貨批量法
經(jīng)濟(jì)訂貨批量法(economic order quantity,EOQ)是一種早在1915年就開(kāi)始使用的批量方法,它假定需求均勻發(fā)生,從而平均庫(kù)存量是訂貨批量的一半。其基本出發(fā)點(diǎn)是使訂貨費(fèi)用和保管費(fèi)用之和最小,如圖5.1所示。
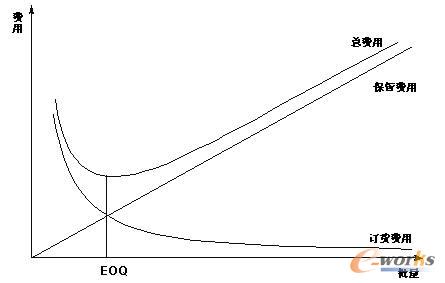
圖5.1 經(jīng)濟(jì)訂貨批量(EOQ)
確定經(jīng)濟(jì)訂貨量EOQ的公式如下:
![]()
式中:R為年需求量,S為一次訂貨費(fèi)用,I為年保管費(fèi)用占平均庫(kù)存值的百分比,C為物料單價(jià)。
假定例中的時(shí)區(qū)單位是月,并假定各種有關(guān)的費(fèi)用數(shù)據(jù)為:S=100,C=50,I=0.24。
年需求量可從9個(gè)月的需求量推算出來(lái),即9∶150=12∶R,求得:R=200。
將這些數(shù)據(jù)代入上式,求得:
![]()
表5.2表示了用EOQ方法確定批量的結(jié)果。
表5.2 經(jīng)濟(jì)訂貨批量法
3. 按需確定批量法
按需確定批量法(lot for lot )是根據(jù)各時(shí)區(qū)的凈需求量來(lái)決定訂貨量,需要多少訂多少,也稱為直接批量法。每當(dāng)凈需求量改變時(shí),相應(yīng)的訂貨量也隨之動(dòng)態(tài)地調(diào)整。采用這種方法也可以降低物料存儲(chǔ)費(fèi)用,因而常用于價(jià)值較高和需求極不連續(xù)的外購(gòu)件及制造件,參考表5.3。
表5.3 按需確定批量法
4. 按固定時(shí)區(qū)的需求量確定批量法
按固定時(shí)區(qū)的需求量確定批量法(fixed period requirements)首先要確定每批訂貨所要覆蓋的時(shí)區(qū)數(shù)。然后,由所覆蓋的幾個(gè)時(shí)區(qū)內(nèi)的需求量來(lái)確定批量。在這里,時(shí)間間隔是常數(shù),而批量是變數(shù),這是和固定訂貨批量法正好相反的。表5.4是按覆蓋2個(gè)時(shí)區(qū)的需求量來(lái)確定批量。
表5.4 按固定時(shí)區(qū)需求量確定批量法
5. 時(shí)區(qū)訂貨批量法
時(shí)區(qū)訂貨批量法(period order quantity,POQ)是一種為適應(yīng)間斷性需求環(huán)境而在EOQ的基礎(chǔ)上修改而得的方法。這種方法首先根據(jù)各時(shí)區(qū)已知的凈需求量數(shù)據(jù),用標(biāo)準(zhǔn)的EOQ方法算出每年的訂貨次數(shù)。然后,用一年的總時(shí)區(qū)數(shù)除以訂貨次數(shù),即得到訂貨的時(shí)間間隔。而每次訂貨覆蓋此間隔內(nèi)的所有需求,如表5.5所示。
表5.5 時(shí)區(qū)訂貨批量法
EOQ=58
一年的時(shí)區(qū)數(shù)=12
年需求量=200
200/58=3.4(每年訂貨約3.4次)
12/3.4=3.5(訂貨間隔為3.5個(gè)月)
6. 最小單位費(fèi)用法
最小單位費(fèi)用法(least unit cost,LUC)與后面要討論的兩種方法有一些共同點(diǎn)。它們都允許訂貨批量和訂貨時(shí)間間隔有變動(dòng),它們都吸取了EOQ中關(guān)于使訂貨費(fèi)用與保管費(fèi)用之和最小的思想,但各自采用的手段多少有點(diǎn)不同。這里要介紹的最小單位費(fèi)用法(LUC)實(shí)際上是一種試探法。為了研究室訂貨批量,LUC首先提出這樣的問(wèn)題:該批訂貨應(yīng)該等于第1進(jìn)區(qū)的凈需求量呢?或是應(yīng)該等于第1、第2兩個(gè)時(shí)區(qū)的凈需求量之和呢?還是應(yīng)該等于第1、第2、第3這三個(gè)時(shí)區(qū)的凈需求量之和?為解決這個(gè)問(wèn)題,LUC要算出以上三種批量對(duì)應(yīng)的“單位費(fèi)用”(即單位訂貨費(fèi)用加上單位保管費(fèi)用)。單位費(fèi)用最小的那個(gè)批量將作為訂貨批量。表5.6說(shuō)明了第1時(shí)區(qū)訂貨批量(45)的計(jì)算過(guò)程,以后的訂貨批量可類似地計(jì)算。其結(jié)果如表5.7所示。
表5.6 最小單位費(fèi)用計(jì)算
表5.7 最小單位費(fèi)用法
7. 最小總費(fèi)用法
最小總費(fèi)用法(least total cost,LTC)所依據(jù)的原理是,當(dāng)計(jì)劃期內(nèi)的訂貨費(fèi)用越接近于保管費(fèi)用時(shí),這個(gè)計(jì)劃期內(nèi)的所有批量的訂貨費(fèi)用與保管費(fèi)用之和也越小。這與EOQ方法所依據(jù)的原理是相同的。為了達(dá)到使總費(fèi)用最小的目的,LTC的具體做法就是選取盡可能使單位訂貨費(fèi)用與單位保管費(fèi)用相接近的訂貨批量。按這樣的觀點(diǎn)再來(lái)看表5.6就會(huì)發(fā)現(xiàn),按LUC方法所選擇的批量(45)所對(duì)應(yīng)的單位訂貨費(fèi)用(2.22),大大超過(guò)了單位保管費(fèi)用(0.22)。
由于LTC方法的目的是使兩種費(fèi)用盡可能接近,所以,可以避免像LUC方法那樣繁雜的計(jì)算過(guò)程。在進(jìn)行LTC計(jì)算時(shí),要用到一個(gè)經(jīng)濟(jì)單位庫(kù)存時(shí)區(qū)量(economic part period,EPP)概念。單位庫(kù)存時(shí)區(qū)是一個(gè)度量單位,類似于“人年”的概念,是指一單位物料在倉(cāng)庫(kù)中存放一個(gè)時(shí)區(qū)。EPP則是指存貯一個(gè)時(shí)區(qū)時(shí)使訂貨費(fèi)用與保管費(fèi)用相等的庫(kù)存量。這個(gè)數(shù)量可以直接用訂貨費(fèi)用除以單位時(shí)區(qū)內(nèi)存貯單位物料的保管費(fèi)用來(lái)求得。在我們的例子中:
![]()
在LTC方法中,選擇單位庫(kù)存時(shí)區(qū)量最接近EPP的訂貨批量。表5.8列出了LTC的計(jì)算過(guò)程。
表5.8 最小總費(fèi)用的計(jì)算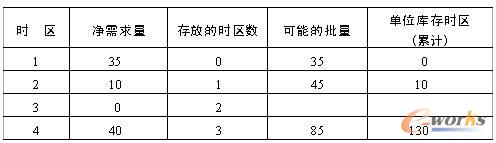
于是,應(yīng)選85為第一個(gè)訂貨批量,這是因?yàn)槠鋵?duì)應(yīng)的單位庫(kù)存時(shí)區(qū)值130比較接近于EPP的值100,這批訂貨可以滿足第1至第5時(shí)區(qū)的需求。用同樣的方法可以確定第二個(gè)訂貨批量為65,可以滿足第6至第9時(shí)區(qū)的需求,如表5.9所示。
表5.9 最小總費(fèi)用法
8. Wagner-Whitin算法
這種方法包含根據(jù)動(dòng)態(tài)規(guī)劃原理制定的一系列優(yōu)化步驟。這些步驟涉及許多數(shù)學(xué)問(wèn)題。概括地說(shuō),這種方法的出發(fā)點(diǎn)是逐一評(píng)審能滿足計(jì)劃期內(nèi)每個(gè)時(shí)區(qū)凈需求量的所有可能的訂貨方案,以便找出對(duì)于整個(gè)凈需求量日程表總體最優(yōu)的訂貨方案。Wagner-Whitin算法的確能使訂貨費(fèi)用與保管費(fèi)用之和最小,所以可用作衡量其他針對(duì)間斷性需求的批量確定方法的標(biāo)準(zhǔn)。這種方法的缺點(diǎn),就是計(jì)算工作量太大,原理也比較復(fù)雜。其具體計(jì)算結(jié)果如表5.10所示。
表5.10 Wagner-Whitin算法
5.3.2 批量調(diào)整因子
不管計(jì)劃訂貨批量是采用哪一種方法確定的,在實(shí)際執(zhí)行時(shí),都會(huì)由于某些因素而必須加以調(diào)整。這時(shí)主要考慮下列幾個(gè)因素:訂貨的上限和下限(或最大訂貨量和最小訂貨量)、報(bào)廢率、批量倍數(shù)。
前面介紹的任何一種批量確定方法在確定批量時(shí)都可能受到訂貨數(shù)量的下限和上限的約束。其中一種下限在前面已經(jīng)提到過(guò),這就是計(jì)算出的訂貨批量至少應(yīng)該等于這批訂貨覆蓋區(qū)間的凈需求量總和。下限和上限可用絕對(duì)的數(shù)字來(lái)表示,也可以用所要覆蓋的時(shí)區(qū)數(shù)來(lái)表示。訂貨的上限和下限通常由管理部門加以限定。
報(bào)廢率,又稱為損耗系數(shù)。在決定訂貨批量時(shí),要按這個(gè)系數(shù)增加一定的余量,以便彌補(bǔ)在加工過(guò)程中可能會(huì)發(fā)生的報(bào)廢或損失,從而保證有足夠數(shù)量的完好成品滿足需求。報(bào)廢率既可以用數(shù)量來(lái)表示,也可以用相對(duì)于訂貨量的百分比來(lái)表示。
批量倍數(shù),可能是出于加工工藝方面的考慮,也可能是出于包裝方面的考慮,使得必須把按批量算法求得的批量向上調(diào)整到某一個(gè)數(shù)的倍數(shù)。例如,批量算法本身是不考慮原材料的下料方式的,因此,所確定的批量可能會(huì)在下料時(shí)產(chǎn)生問(wèn)題。如果在為某種制造項(xiàng)目下料時(shí),一定尺寸的鋼板恰好切成9塊料,而由批量算法算出的訂貨批量是30,那么在下料時(shí)第4塊鋼板就會(huì)出現(xiàn)零頭。為了避免這種情況,則應(yīng)把訂貨批量調(diào)整為36(此時(shí)的最小訂貨量是9)。又如,在采購(gòu)的情況下,對(duì)于我們要采購(gòu)的某項(xiàng)物料,供應(yīng)商是裝箱賣的,25件裝一箱,最少買兩箱。于是,批量倍數(shù)為25,最小訂貨量是50。
在需要對(duì)一項(xiàng)物料的訂貨進(jìn)行多種調(diào)整的情況下,這些調(diào)整是按一定的邏輯性順序進(jìn)行的。舉例來(lái)說(shuō),如果某批訂貨按批量算法確定的批量為173,這個(gè)批量可以滿足5個(gè)時(shí)區(qū)的需求。但是,管理部門提出每批訂貨最多覆蓋3個(gè)時(shí)區(qū)。此外,還要考慮報(bào)廢率以及批量倍數(shù)(每單位的原材料可下料20件)。這樣一來(lái),最初確定的173件的批量就要按下面的順序進(jìn)行調(diào)整:

采用批量調(diào)整因子會(huì)增加問(wèn)題的復(fù)雜程度。我們以最小訂貨量來(lái)說(shuō)明這個(gè)問(wèn)題。假定生產(chǎn)產(chǎn)品A要用到物料B、C、D,其中,物料B是產(chǎn)品A的子項(xiàng),每個(gè)A用到1個(gè)B;物料C是物料B的子項(xiàng),每個(gè)B用到1個(gè)C;物料D是物料C的子項(xiàng),每個(gè)C用到1個(gè)D。A、B、C、D的最小訂貨量分別是100、400、600和1000。如果接到產(chǎn)品A的客戶訂單為200件,且A、B、C、D的庫(kù)存量均為0,那么,對(duì)A、B、C、D的生產(chǎn)訂單量分別為200、400、600和1000。滿足客戶需求后,A、B、C、D的庫(kù)存量分別為0、200、200、400。
如果下一個(gè)客戶訂單數(shù)量為100件,那么,只對(duì)產(chǎn)品A下達(dá)生產(chǎn)訂單100件即可。滿足客戶需求后,A、B、C、D的庫(kù)存量分別為0、100、200、400。
如果這份客戶訂單的數(shù)量不是100件而是300件,則情形就大不相同了。這時(shí)必須對(duì)A、B、C、D分別下達(dá)生產(chǎn)訂單,數(shù)量分別為300、400、600和1 000。滿足客戶需求后,A、B、C、D的庫(kù)存量分別為0、300、400、800。
由此可以看出,當(dāng)考慮批量因子時(shí),不但會(huì)導(dǎo)致庫(kù)存剩余,而且使得庫(kù)存的管理變得復(fù)雜。因此,以手工作業(yè)的方式是很難做好的。換言之,在這種情況下,MRP系統(tǒng)是不可或缺的管理工具。MRP系統(tǒng)不但很容易把這些數(shù)據(jù)計(jì)算清楚,而且可以很快把庫(kù)存剩余分配給后面接踵而來(lái)的毛需求量。所以,雖然由于考慮批量造成的庫(kù)存剩余是難免的,但不必?fù)?dān)心它們會(huì)越積越多。
在確定批量規(guī)則和調(diào)整因子時(shí),還應(yīng)當(dāng)注意物料是處于物料清單的上層還是下層。對(duì)處于上層的物料,要特別慎重,以免形成連鎖反應(yīng),造成太多的庫(kù)存剩余。這同確定安全庫(kù)存的道理是一樣的。
5.4 安全庫(kù)存和安全提前期
由于大量不確定因素的存在,需求和供應(yīng)總是難免有不平衡的情況。為了彌補(bǔ)可能出現(xiàn)的不平衡,需要在供需之間增加緩沖的手段:一種是安全庫(kù)存,靠增加一定的庫(kù)存量來(lái)起到緩沖的作用;另一種是安全提前期,靠供應(yīng)時(shí)間上的余量來(lái)起到緩沖的作用。兩種安全參數(shù)都是為了提高客戶服務(wù)水平。
5.4.1 安全庫(kù)存概述
安全庫(kù)存可以用來(lái)作為應(yīng)對(duì)意外的供需差異的緩沖方法。如果供應(yīng)商的交貨數(shù)量少于需求,如果生產(chǎn)車間生產(chǎn)的零件有缺陷,或者如果需求預(yù)測(cè)是10件,而接到的客戶訂單卻要求12件,則可用安全庫(kù)存來(lái)滿足需求的差異。但是,安全庫(kù)存的使用必須謹(jǐn)慎。
設(shè)置安全庫(kù)存無(wú)疑要增加庫(kù)存管理的成本,所以在物料清單的那個(gè)層次上設(shè)置安全庫(kù)存應(yīng)當(dāng)慎重考慮。以下是一些可供選擇的策略。
·對(duì)于提前期很長(zhǎng)的物料設(shè)置安全庫(kù)存。這樣可以縮短產(chǎn)品的累積提前期。
·對(duì)選項(xiàng)設(shè)置安全庫(kù)存。有時(shí)在一個(gè)產(chǎn)品族中有很多產(chǎn)品,這些產(chǎn)品是由基本配置和眾多的不同選項(xiàng)構(gòu)成的。在這種情況下,對(duì)產(chǎn)品族作預(yù)測(cè)往往要比對(duì)具體的產(chǎn)品作預(yù)測(cè)更準(zhǔn)確。而對(duì)產(chǎn)品族作預(yù)測(cè)本質(zhì)上是對(duì)產(chǎn)品的基本配置作預(yù)測(cè),所以意外情況多出現(xiàn)在選項(xiàng)上。因此,對(duì)選項(xiàng)設(shè)置安全庫(kù)存是適當(dāng)?shù)摹?/P>
·對(duì)于用戶希望隨時(shí)都有的產(chǎn)品設(shè)置安全庫(kù)存。在很多情況下,客戶希望生產(chǎn)商的某些產(chǎn)品隨時(shí)都有,如果沒(méi)有,客戶會(huì)感到失望和不可接受。但是,對(duì)另外一些產(chǎn)品,如果客戶買不到則不會(huì)產(chǎn)生強(qiáng)烈的不滿。
【例5.2】在一個(gè)汽車維修站,客戶希望汽油以及某些汽車配件,如風(fēng)扇皮帶、濾油器等,隨時(shí)都有,而不愿意等待;如果要更換電池或者火花塞,客戶或許愿意等一天或兩天;但是,如果客戶要求為一輛1975年生產(chǎn)的福特牌汽車更換零件,如果維修站沒(méi)有,客戶則不會(huì)感到強(qiáng)烈的不滿。所以,對(duì)于用戶希望隨時(shí)都有的產(chǎn)品,應(yīng)當(dāng)設(shè)置安全庫(kù)存。
為了介紹安全庫(kù)存和凈需求的關(guān)系,讓我們回憶一下在第2章介紹的計(jì)算凈需求的方法。
按下面公式求各時(shí)區(qū)的預(yù)計(jì)可用量:
某時(shí)區(qū)預(yù)計(jì)可用量=上時(shí)區(qū)預(yù)計(jì)可用量+該時(shí)區(qū)計(jì)劃接受量-該時(shí)區(qū)毛需求量
當(dāng)預(yù)計(jì)可用量出現(xiàn)負(fù)值時(shí),就意味著出現(xiàn)凈需求,其值等于這個(gè)負(fù)值的絕對(duì)值。
但是,如果對(duì)相應(yīng)的物料設(shè)置了安全庫(kù)存,最后的結(jié)論就應(yīng)當(dāng)改成“當(dāng)預(yù)計(jì)可用量低于安全庫(kù)存時(shí),就意味著出現(xiàn)凈需求,其值等于安全庫(kù)存與預(yù)計(jì)可用量的差”。
由此可以看出,在ERP系統(tǒng)中,對(duì)安全庫(kù)存的處理邏輯與對(duì)毛需求的處理邏輯是相似的,而原來(lái)關(guān)于凈需求的結(jié)論不過(guò)是現(xiàn)在的結(jié)論當(dāng)安全庫(kù)存為零時(shí)的特例。
5.4.2 如何設(shè)置安全庫(kù)存
為物料設(shè)置適當(dāng)?shù)陌踩珟?kù)存量涉及實(shí)際需求相對(duì)于需求預(yù)測(cè)的偏差的度量。
假定實(shí)際需求的發(fā)生服從以預(yù)測(cè)值為均值的正態(tài)分布,通過(guò)正態(tài)分布的標(biāo)準(zhǔn)差σ可以表示適當(dāng)?shù)陌踩珟?kù)存量。我們稱實(shí)際需求值和預(yù)測(cè)值的差為偏差。標(biāo)準(zhǔn)差σ可通過(guò)如下公式來(lái)計(jì)算:

式(5.1)中,n是用來(lái)觀測(cè)實(shí)際需求值的時(shí)區(qū)數(shù)。但是,根據(jù)數(shù)理統(tǒng)計(jì)小樣本推斷的理論,當(dāng)n<30的時(shí)候,采用如下公式:

在實(shí)踐中,用來(lái)觀測(cè)實(shí)際需求值的時(shí)區(qū)數(shù)往往是小于30的,所以常采用式(5.2)。
【例5.3】根據(jù)表5.11所示的數(shù)據(jù),求對(duì)應(yīng)的標(biāo)準(zhǔn)差。
表5.11 某產(chǎn)品的預(yù)測(cè)需求值、實(shí)際需求值、偏差和偏差的平方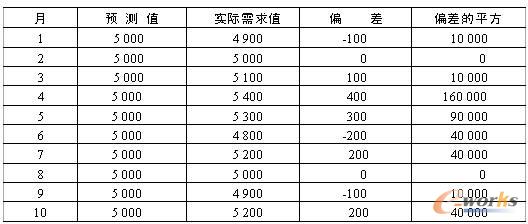
根據(jù)表5.11的數(shù)據(jù),可以求得10個(gè)時(shí)區(qū)偏差平方之和為400 000,于是:
![]()
概率論的基本知識(shí)告訴我們,當(dāng)實(shí)際需求的發(fā)生服從以預(yù)測(cè)值為均值的正態(tài)分布時(shí),實(shí)際需求發(fā)生在±σ之間的概率為68.26%,實(shí)際需求發(fā)生在±2σ 之間的概率為95.44%,實(shí)際需求發(fā)生在±3σ 之間的概率為99.74%。如圖5.2所示。
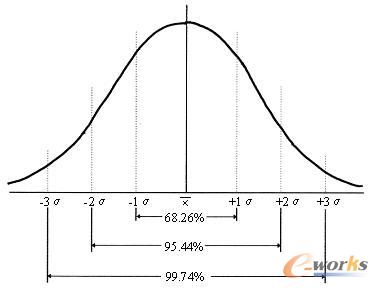
圖5.2 正態(tài)分布圖
如果庫(kù)存量等于預(yù)測(cè)值,那么可用庫(kù)存量滿足需求的概率是50%。換言之,庫(kù)存服務(wù)水平是50%,如圖5.3陰影部分所示。
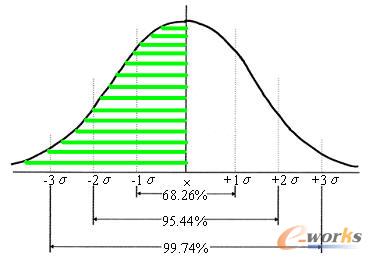
圖5.3 不設(shè)置安全庫(kù)存情況下的庫(kù)存服務(wù)水平
如果我們想提高庫(kù)存服務(wù)水平,就要借助于安全庫(kù)存。如果保持1σ的安全庫(kù)存,庫(kù)存服務(wù)水平將是84.13%(=50%+68.26%/2),如圖5.4陰影部分所示。
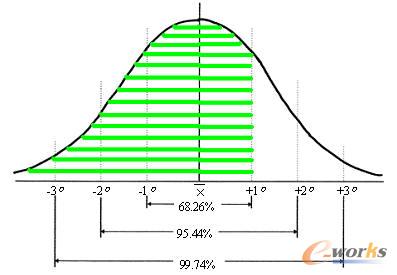
圖5.4 安全庫(kù)存為1σ情況下的庫(kù)存服務(wù)水平
類似地,如果保持2σ 的安全庫(kù)存,庫(kù)存服務(wù)水平將是97.72%。如果保持3σ 的安全庫(kù)存,庫(kù)存服務(wù)水平將是99.87%。
更一般的結(jié)果如表5.12所示(假定σ=211)。
表5.12 庫(kù)存服務(wù)水平和安全庫(kù)存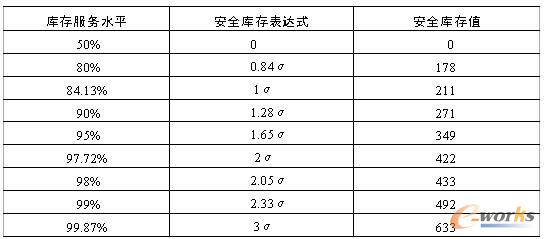
在表5.12中,安全庫(kù)存表達(dá)式中σ前面所乘的系數(shù)稱為庫(kù)存安全系數(shù)。安全系數(shù)可以通過(guò)查詢標(biāo)準(zhǔn)正態(tài)分布表而得到。在標(biāo)準(zhǔn)正態(tài)分布表中,以所希望的庫(kù)存服務(wù)水平作為函數(shù)值,反查對(duì)應(yīng)的自變量值即是安全系數(shù)。
現(xiàn)在,可以總結(jié)根據(jù)所希望的庫(kù)存服務(wù)水平確定安全庫(kù)存量的方法如下:
(1)根據(jù)需求的預(yù)測(cè)值和n個(gè)時(shí)區(qū)的需求實(shí)際發(fā)生值,利用本節(jié)給出的公式求得正態(tài)分布的標(biāo)準(zhǔn)差σ。
(2)根據(jù)所希望的庫(kù)存安全水平,反查正態(tài)分布表,得到庫(kù)存安全系數(shù)。
(3)將庫(kù)存安全系數(shù)乘以標(biāo)準(zhǔn)差σ,得到所需要的安全庫(kù)存值。
5.4.3 安全提前期
安全提前提期和安全庫(kù)存的作用是類似的,都是為了緩沖供需的不平衡性。一般來(lái)說(shuō),安全庫(kù)存是針對(duì)供需數(shù)量不確定性比較大的物料,如備品備件以及面向訂單裝配產(chǎn)品的公用件和可選件。對(duì)供需時(shí)間的不確定性,如受運(yùn)輸或其他因素影響,不能如期抵達(dá)的采購(gòu)件或完工產(chǎn)品,則會(huì)采用安全提前期。
同安全庫(kù)存相比,安全提前期占用資金比較少,但是如果提前的日期設(shè)置不當(dāng),有時(shí)會(huì)因提前期的誤差影響優(yōu)先級(jí)的計(jì)算。在庫(kù)存資金占用相近的情況下,安全庫(kù)存對(duì)滿足客戶服務(wù)水平更有保證,系統(tǒng)的處理也更簡(jiǎn)單。
轉(zhuǎn)載請(qǐng)注明出處:拓步ERP資訊網(wǎng)http://www.guhuozai8.cn/
本文標(biāo)題:ERP原理與應(yīng)用教程 連載六
本文網(wǎng)址:http://www.guhuozai8.cn/html/consultation/1082064133.html