一.前言
降落傘包裝體積小、減速效果好,在航空、航天減速系統中有著不可取代的地位。在降落傘的折疊展開過程中,其阻力面積急劇增大至幾百倍,是一個典型的流場結構相互作用的強非線性問題,涉及到空氣動力學、紡織材料結構力學、多體運動動力學等諸多力學問題,研究難度很大。因此,過去一直將降落傘的折疊展開過程分為拉直和充氣兩個階段。
早期的降落傘拉直過程理論模型為兩質點平面模型,只能得到物、傘兩質點的運動參數。1984年,Purvis基于繩索動力學理論,首次提出了拉直過程的離散模型,模型中將柔性大變形的傘繩、傘衣、連接帶離散成若干繩段(質點),各繩段的運動由它們的重力、氣動力和張力確定;文獻對Purvis模型進行了不同方面的改進,形成了較為完善的多質點、多剛體、多自由度拉直過程運動模型,但無法反映織物折疊展開過程中材料的結構特性和周圍流場的氣動特性。
降落傘充氣過程的理論模型一直是基于半經驗半理論方法進行研究,主要方法有充氣距離法、充氣時間法和動量方法。1981年,Purvis最早對平面圓傘軸對稱面進行了二維流固耦合計算,但對傘衣結構模型和傘衣內部流場壓力模型做了非常大的簡化,且對阻尼系數較為敏感;1993年,Benny,Stein等人提出了降落傘CFD/MSD耦合模型,該模型一定程度上反映了傘衣展開過程中流場結構相互作用的物理本質,但由于傘衣織物為質點模型,無法得到傘衣充氣過程中的結構力學性能,并且沒有和試驗結果進行對比;2005年起,Benjamin等人采用任意拉格朗日-歐拉法(Arbitrary Lagrange Euler Method,ALE)模擬了三維降落傘開傘過程,并經過了試驗驗證。國內,秦子增、曹義華、余莉等人也做了大量的研究工作,主要側重對結構動力學行為或者流場行為來研究降落傘的充氣過程,大多停留在二維水平,三維研究還處于摸索階段。
前人的研究工作為本文的研究打下了寶貴的基礎,但也發現降落傘從拉直到充氣是一個完整的流場與結構相互作用過程,而現有研究成果均忽略了它們之間的聯系,無法解決從降落傘初始折疊狀態到傘衣完全充滿整個過程中的流場結構耦合數值計算問題,對實際工程中出現的一些失效現象無法解釋。本文基于ALE方法進行折疊降落傘的展開充氣過程的流固耦合計算,獲得了結構和流場的動態變化過程,結果證明了引導傘經驗設計的有效性,但存在局限性,個別情況下經驗設計將導致不良充氣狀態的產生。
二.計算模型
1.數學模型
針對降落傘,進行開傘計算仿真,本文采用了ALE方法進行流固耦合計算。流場控制方程可表示為:
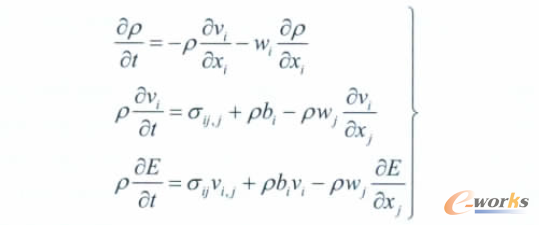
式中ρ為流場密度;t為時間;vi為物質速度;wi為相對速度wi=vi- ûi,ûi為網格速度;xi為i向歐拉坐標;σij為應力張量σij=-pδij+μ(vi,j+vj,i),p為壓力,μ為動力粘度,δij表示Kroneckerδ-函數;bi為單位體積力;E為能量。
其中,網格控制方程為:
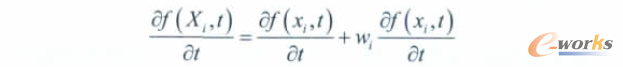
式中Xi表示拉格朗日坐標。
結構域控制方程:
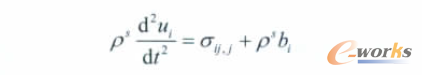
式中ui為結構域中節點位移;ρs表示結構密度。
通過對上述控制方程的耦合計算來實現流固耦合,采用中心差分法時間顯式法進行求解,流場域和結構域的速度和位移分別按以下等式更新:
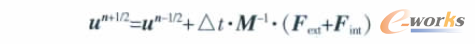
式中u為速度矢量;Fint為內力矢量,Fext為外力矢量,它們與體力和邊界條件相關聯;M為質量對角矩陣。
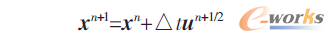
式中x為位移矢量。
本文采用罰函數進行結構與流場的耦合,根據耦合點距離d計算界面力Fc(Fc=k·d,其中k為剛度系數),將Fc作為外部力Fext的一部分,對耦合區域的速度、位移進行調整。
2.仿真模型
本文的計算模型為考慮織物透氣量的平面圓形傘:傘衣幅數為8塊,傘繩長LS=750mm,傘衣總面積為A=0.3m2,基于初始矩陣修正的直接折疊方法建立了降落傘的“Z”型折疊模型,并由引導傘將折疊傘衣拉入外部流場,見圖1。

圖1 降落傘有限元模型
目前,引導傘的設計均采用經驗方法,有關文獻列出了引導傘的經驗設計,本文為驗證這些經驗設計研究了不同引導傘面積對主傘拉直過程的影響,將引導傘的作用折算成定常力FY:
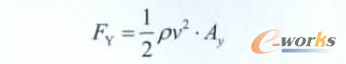
式中v為拉直速度;Ay為引導傘面積。
表1為本文各計算模型工況及引導傘作用力,其中,*表示經驗設計值:拉直速度<370km/h,則引導傘面積/主傘面積=3%。
表1 各計算算例來流速度及引導傘大小

三.計算結果與分析
計算結果如圖2至圖5所示,其中圖2為上述模型的動態變化過程,圖3和圖4分別為各個模型的動載和投影直徑變化,圖5為模型2在拉直和充氣過程中的流場速度矢量圖。
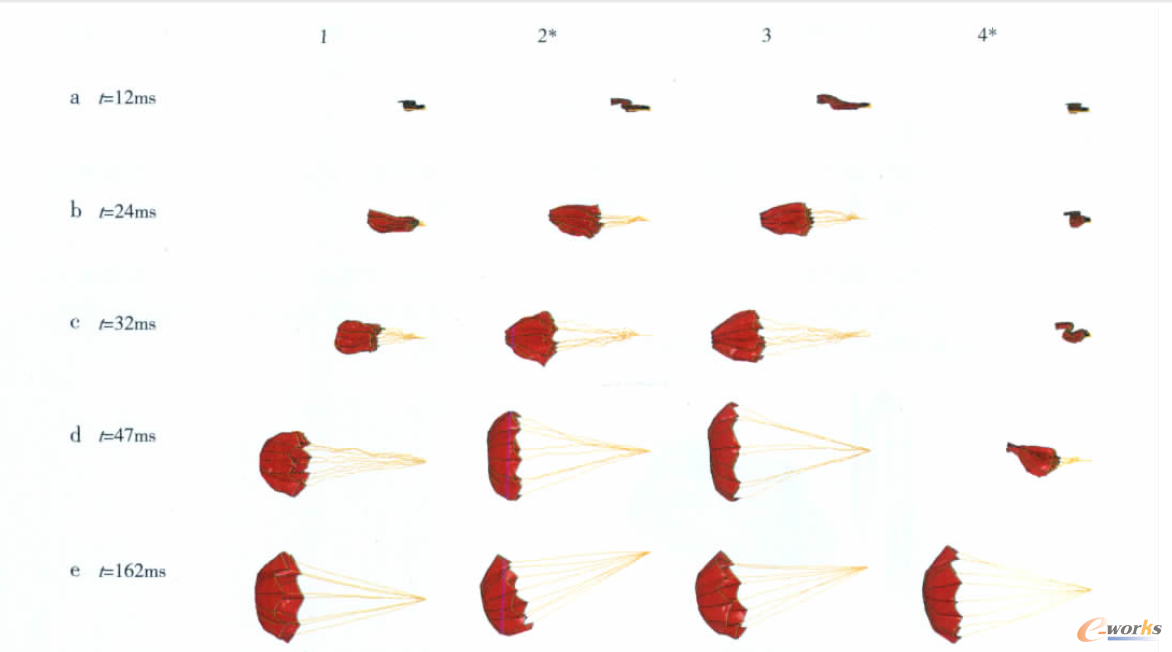
圖2 各模型動態開傘變化過程
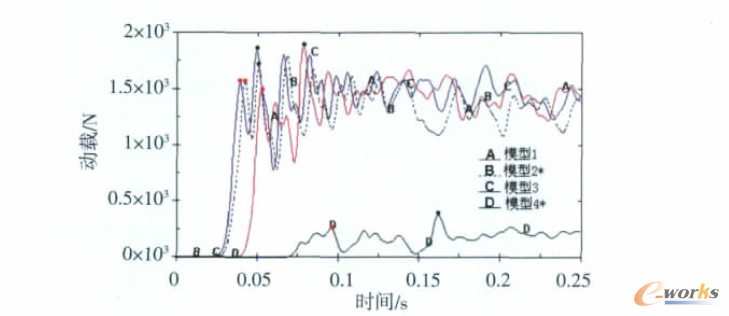
圖3 開傘動載變化
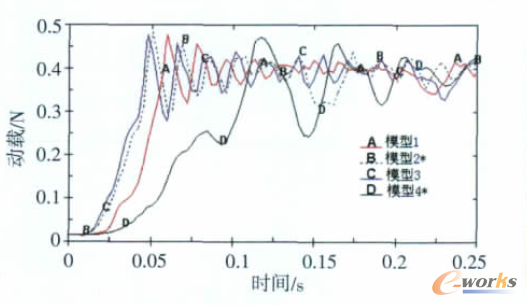
圖4 投影直徑變化
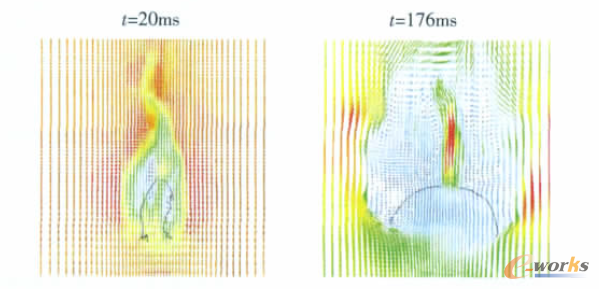
圖5 模型2 流場速度矢量
計算結果表明:模型2在拉直階段始終保持傘衣拉直(在圖2的b2至c2階段由于無傘衣套約束,傘衣底部部分打開),至42ms時傘繩首次實現拉直,并第一次達到動載極大值,見圖3;隨后傘衣開始充氣,50ms左右動載達到最大值,充氣完成;隨后,傘衣出現有規律的“呼吸”現象和擺動,見圖2的e2階段,“呼吸”現象并且逐漸穩定,見圖4。
模型3開傘情況與模型2類似。但模型1在拉直過程中由于引導傘面積過小,產生的拉直力無法保持傘衣拉直狀態,傘頂出現明顯充氣現象,見圖2的c1階段,雖然傘衣未進一步展開,但是在拉直過程中該局部充氣已經造成傘衣非對稱充氣形狀的形成,見圖2的d1階段,非對稱充氣形狀直接導致充氣時間明顯過長,見圖3;同樣采用經驗公式設計引導傘的模型4在40m/s風速條件下,拉直初始階段就發生明顯的局部非對稱充氣,見圖2的d4階段。
以上算例再次證明:引導傘要提供足夠的拉力,保證傘系統沿全長拉直,防止不良充氣現象的產生,但是過大的引導傘又會增加傘系統體積和質量;傳統的經驗設計過于粗糙,個別情況下,設計效果不明顯,容易導致不良充氣狀態,反而將大大增加反復實物試驗人力、資金投入。
此外,從流場結果可以發現(圖5,左邊的拉直階段;右邊的充氣階段):拉直階段流場很少出現大尺度渦結構,而傘衣幅運動以引導傘拉力影響為主,呈松弛狀態,結構與流場相互影響較小;而在充氣階段,隨著傘衣的逐漸充滿,傘頂上方的一對渦不再保持對稱,而隨傘體擺動而變化,大尺度渦結構的變化表明結構與流場相互影響較大。這也說明多體動力學模型計算拉直過程是可行的,但局限于拉直過程中結構與流場相互影響較小的情況,如模型2。
四.結束語
本文采用ALE方法進行開傘數值仿真,獲得結構和流場動態結果,通過結果對比發現經驗設計存在一定的局限性,而流場結果說明了多體動力學模型計算拉直過程局限于拉直過程中結構與流場相互影響較小的情況。本文的研究方法對完全折疊降落傘開傘過程仿真具有借鑒意義。
核心關注:拓步ERP系統平臺是覆蓋了眾多的業務領域、行業應用,蘊涵了豐富的ERP管理思想,集成了ERP軟件業務管理理念,功能涉及供應鏈、成本、制造、CRM、HR等眾多業務領域的管理,全面涵蓋了企業關注ERP管理系統的核心領域,是眾多中小企業信息化建設首選的ERP管理軟件信賴品牌。
轉載請注明出處:拓步ERP資訊網http://www.guhuozai8.cn/
本文標題:折疊降落傘展開過程研究