0 引言
產品裝配序列規劃作為產品生命周期的重要一環,在產品設計開發過程中占有很重要的地位,因為產品設計總費用40%~60%被花費在裝配勞動中,如何在給定產品在設計方案的條件下,尋找滿足幾何約束以及其它約束條件(工藝、裝配成本等)的合理可行的裝配序列一直是裝配工藝師所面臨的富有挑戰性的工作。好的裝配序列規劃已經被視為減小裝配難度、減少裝配工具以及縮短裝配時間的實用方法。裝配序列規劃問題的本質是一個NP組合優化難題,傳統的裝配序列規劃的方式有兩種:一是基于裝配工程師的知識以及經驗,二是圖搜索算法。方法一受設計者的知識局限性和主觀性影響較大,尤其是對于復雜零件的裝配工藝,設計出的裝配序列常常不是最優的,甚至是不可行的。方法二的局限性在于當產品零件數目較多時,將會出現裝配序列組合爆炸的問題。20世紀90年代以來,人工智能被運用到組合優化求解問題中,并取得了一些成就。包括模擬退火算法、人工神經網絡、蟻群算法、遺傳算法及其相關混合算法。因遺傳算法具有搜索速度快、算法簡單,無需遍歷整個解空間就能找到一個最優或次最優解,能有效解決組合優化中得組合爆炸問題,修改染色體的編碼方式和適應度函數可解決不同的優化問題等特點,遺傳算法被廣泛的運用到裝配序列規劃問題的求解。
1 零件可行裝配方向推理及裝配基準件選擇
1.1 遺傳算法的相關研究及改進
Bonnevil等首先將遺傳算法引入裝配規劃設計中,但他們的算法效果受初始迭代值的影響,而且要求初始序列都是有效的;Romeo M Marian等在建立關聯矩陣和優先關系矩陣的基礎上,通過向導搜索算法生成可行的裝配序列后,再用遺傳算法對可行的裝配序列進行優化,該方法也要求初始序列都是有效的;楊鵬等改進了傳統的基因算法,通過交叉和多層次變異來實現基于基因組編碼表示的多信息裝配序列的并行優化;周開俊等在楊鵬的研究基礎上考慮子裝配體穩定性的目標函數,采用帶記憶的遺傳算法進行裝配序列規劃;劉誠等將遺傳學原理的基因修復技術引入用于求解裝配序列規劃問題的遺傳算法,利用基因“修復”操作,將子代個體中違反先序約束的基因“修復”為有效基因,從而保證了整個種群的基因多樣性,避免了進化過早地收斂于局部最優解。基于幾何干涉矩陣的基礎推導并優化裝配序列,但是忽視了裝配過程中裝配基準和零件裝配優先關系。
有鑒于此,采用改進的遺傳算法,考慮裝配基礎件對產品的裝配序列進行規劃研究。通過該算法,獲得一條滿足幾何約束、符合實際裝配過程的高效率產品裝配序列,用以指導產品的實際裝配。
1.2 零件裝配方向推理和可行性判斷
在笛卡兒直角坐系下,零部件的裝配方向采用該坐標系的坐標軸方向,一個裝配序列的幾何可行性是指:至少存在一個坐標軸方向使得將某一零部件裝配到位時,而不與其他已裝配好的零部件發生干涉。為評價裝配序列的幾何可行性,采用干涉矩陣I描述裝配過程中零部件間的幾何優先關系。
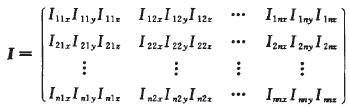
假定有n個零件參與裝配,那么干涉矩陣是一個n行、3×n列的矩陣,3代表零件在+X、+Y、+Z的3個裝配方向。其元素Iijx表示了零件j沿+X方向裝配時與零件i的干涉情況,判定規則如下:如果零件j沿+X方向裝配到位與零件i發生干涉,則Iijx=1;反之則Iijx=0。零件j沿-X方向裝配與零件i干涉的情況即Iij-x,與零件i沿+X方向裝配與零件j干涉的情況相同,由元素Iijx表示,規定Ii=0。同理,可以確定Iijy和Iijz的值。
現設{P1,P2,…Pm}為零件Pi裝配前已經裝配完的零件序列,則零件Pi的可行裝配方向可由式(1)~式(6)判定。
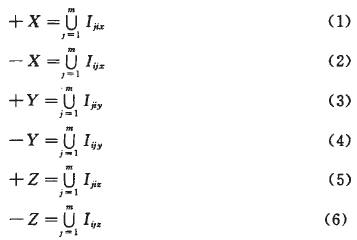
其中,I[i][j]對應干涉矩陣中的元素,U表示矩陣元素求或運算,I的維數取決于裝配的維數,二維的情況取2,三維的情況取3。對于序列{P1,P2,…,Pm,Pi}是否為幾何可行裝配序列取決于式(1)~式(6)的結果,當式(1)~式(6)中至少存在一個為零時,例如式(1)的結果為0,則說明Pi可從+X方向裝配到位而不與P1,P2,…,Pm發生干涉,反之,若式(1)~式(6)的結果全不為零,則P1,P2,…,Pm,Pi是不可裝配的。
1.3 裝配基準件的選擇
1.1節從幾何角度上推理了零件的裝配方向,其并不涉及裝配初始零部件。現實產品裝配過程中,通常會裝配一個零件固定不動,其余零部件均以該零件為裝配基準進行裝配。一個裝配體包含n個零件,所有可能的裝配序列為,n!個,當指定了基準件后可能的裝配序列為(n-1)!,搜索空間變為以前的1/n。可見基準件最先裝配作為一條啟發式規則可以在很大程度上減小搜索空間,提高裝配序列生成的效率。基準件的選取對裝配操作的難度、裝配夾具的設計等產生重大的影響,基準件的選擇一般遵循以下幾個原則:與其它零件連接數多;重量大、重心低;體積大;剛性大;一般避免選用易碎的、貴重的零件做基準件,例如傳動軸、齒輪等。
2 基于遺傳算法的裝配序列規劃方法
在考慮基礎件的情況下,設計了相應的交叉算子、變異算子和適應度函數,對產品的裝配序列進行規劃,用以獲得滿足相關約束條件的裝配序列。
2.1 編碼
采用實數序列的遺傳算法編碼求解產品裝配序列規劃問題,染色體的一個基因用以編碼一個待裝配零部件,每個基因所在染色體的位置代表了相應待裝配零部件的在該裝配順序中的位置。群體的初始化、交叉操作及變異操作中各零件的序號僅出現.一次。例如染色體3-1-4-2-6-5-9-8-7,該染色體首先裝配的零部件為3,其后,裝配零部件1,依此類推。
2.2 交叉算子
采用如下的部分交叉重組方法,具體方式如下。
a.隨機在種群中選擇2條染色體A,B,隨機在染色體中選擇一個交配區域。2父染色體及交配區域選定為:

b.將B的交配區域加到A的交叉點后,將A的交配區域加到B的交叉點后得到:

c.在A',B'中依次刪除與交配區相同的零部件編碼得到最終的2子染色體為:

這種交叉方法在能夠確保基準件的位置在染色體的最前端。
2.3 變異算子
每一代種群以機率Pm進行變異,一旦變異操作發生,隨機挑選K條染色體進行變異,且當染色體的基因個數為奇數時,從該染色體的第二位基因開始.每相鄰2個基因前后交換;當染色體的基因個數為偶數時,從該染色體的第三位基因開始,每相鄰2個基因前后交換。通過這樣的變異操作不僅最大限度地打破了裝配序列的排列順序,同時能夠確保基準件的位置在染色體的最前端。
2.4 適應度函數設計
遺傳算法中適應度函數的設計將待求解問題的目標函數與種群的每個個體聯系起來,通過將待求解問題的目標函數轉化為適應度函數,再通過適應度函數求得個體的適應度,適應度值高的個體遺傳到下一代的幾率較大,反之,適應度值低的個體遺傳到下一代的幾率較小。影響裝配效率的因素很多,僅從裝配方向的改變次數、裝配工具的更改次數、子裝配的穩定性、基準件的位置四個方面考慮設計適應度函數。
a.裝配換向次數C。對某一給定裝配序列,由1.1節可以推理零部件的裝配方向。當相鄰的2個零部件裝配方向改變時,序列的裝配換向次數加1。該指標反映了裝配操作的復雜性信息。
b.裝配工具的更換次數To通過判斷相鄰2個零部件裝配時所使用的裝配工具是否相同,累加計算出給定裝配序列的裝配工具改變次數,該指標量化表示了裝配序列的聚合性。T越小,裝配工具更換的次數越小,裝配效率越高。
c.裝配體的穩定性。它是指某一裝配操作所涉及的2個子裝配體在重力和建立裝配所需力的作用下,保持各自內部裝配關系的能力。定義穩定聯接矩陣SN×N,其中矩陣元素Sij表示零部件i與零部件j之間的聯接關系,當i與j存在穩定聯接關系時Sij=2,當i與j存在接觸聯接關系時Sij=1,當i與j不存在聯接關系時Sij=0。穩定聯接指有強制約束零件之間相互移動的聯接,包括螺紋聯接、軸與孔的過盈聯接、O型圈聯接和卡簧聯接。則一個裝配序列的裝配穩定性就可以用1×(N-1)的向量K={k2,k3,…,kn},其值S如式(7)所示。裝配體的穩定性直接影響到裝配操作的可靠性、夾具和工具的復雜性。

式中,n為裝配零件總數;S值越大裝配序列的穩定性越好,0≤S≤2n-2。
d.基準件的位置。如1.3節所述,基準件的裝配應該在第一位,在初始種群中存在滿足幾何約束的裝配序列,但是居首的零件并非裝配基準件,則需要對裝配基準件居首的可行裝配序列與裝配基準件非居首的可行裝配序列予以區分。通過區分,一方面能保持種群的多樣性;另一方面對裝配基準件居首的可行裝配序列的適應度值予以加權,提高該序列的適應度值,保證其在種群中的競爭性。
綜上所述,適應度函數設計如下:
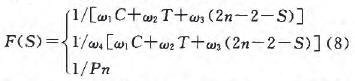
式中,S為種群的各裝配序列,當裝配序列滿足幾何約束且基礎件位置位于序列非首位時取式(8)第1式,當裝配序列滿足幾何約束且基礎件位置位于序列首位時取式(8)第2式,當裝配序列不滿足幾何約束式(8)第3式;F(S)為裝配序列的適應度函值;ω1,ω2,ω3,ω4為權重系數;P為懲罰系數,根據經驗,取ω4=0.8,ω1+ω2+ω3=1,取P=2。
3 遺傳算法執行步驟
按照遺傳算法的一般思路,結合裝配序列規劃應用的實際情況,在考慮基準件的基礎上,該算法步驟如下:
步驟1。設定初始種群大小pop、交叉概率Pc、基因組變異概率Pm。
步驟2。確定初始種群并將其作為最初的父代種群;先隨機生成初始種群,然后,在DELMIA軟件中通過虛擬拆卸的方式獲得一些裝配序列,最后,將通過虛擬拆卸的方式獲得的這些裝配序列隨機替換初始種群的裝配序列,將替換后的種群作為最初的父代種群。
步驟3。根據事先建立的裝配體干涉矩陣,先從幾何約束角度判斷初始種群中個體的可行性,再對幾何約束可行的個體判斷居首位置的零件判斷是否為基準件,最后根據式(8)分別計算初始種群個體的適應度值。
步驟4。確定個體選擇算法,選擇輪賭盤選擇方法。
步驟5。當優化結果不滿足終止條件時。
a.從群體中隨機兩兩選擇出不同個體作為親本,用交叉概率來確定染色體是否進行交叉操作。
b.用變異概率來確定染色體是否進行了交叉操作。
c.用交叉和變異產生與父代相同個數的子代。
d.同步驟3判斷新個體的可行性,計算新個體的適應值。
e.通過選輪賭盤選擇方法得到pop個新的個體,并用這些新的個體更新原始種群。
步驟6。當迭代次數達到預先設定的某值時,輸出適應度值最高的個體,即為優化的裝配序列。算法流程圖如圖1所示。
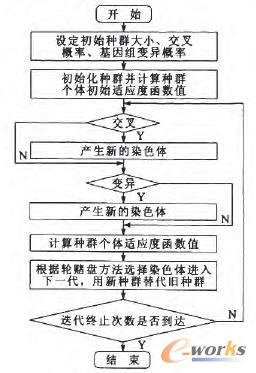
圖1 算法流程
4 實例驗證
為驗證算法的有效性,采用Matlab編程軟件驗證分析裝配基準件的改進遺傳裝配序列規劃算法,并以如圖2所示的某鏈輪為例進行了裝配仿真驗證,出于驗證過程的簡便化目的,對鏈輪做了以下簡化:①由于鏈輪的對稱結構,故只考慮了鏈輪一側的裝配,如圖3所示;②規劃過程中未出現子裝配體的裝配過程;③螺栓一般只考慮一組。初始種群中的個體均以隨機的方式產生,并加入由DELMIA軟件虛擬拆卸得到的可行裝配序列,用以改善裝配序列種群的組成成份。在程序運行時,初始種群的規模pop=50,迭代條件設定為gmax=50,交叉概率和變異概率(Pc,Pm)分別取0.8,0.1。最終規劃出的鏈輪裝配序列如表1所示,圖4為pop,Pc,Pm分別取50,0.8,0.1時各代種群的平均適應度函數值圖,該序列的適應度函數值是0.1866。
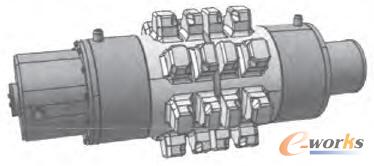
圖2 鏈輪
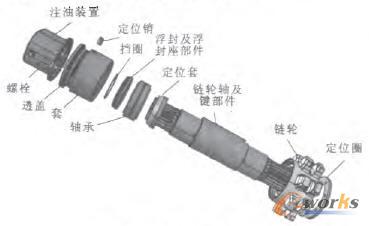
圖3 鏈輪左側爆炸圖
表1 裝配序列規劃結果
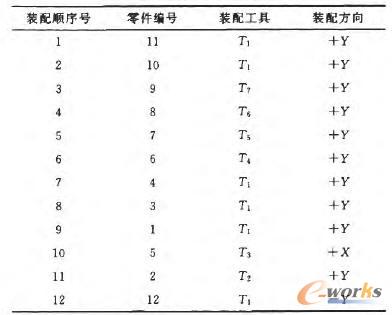
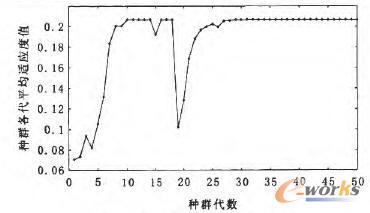
圖4 種群各代平均適應度值
5 結束語
在考慮裝配基準件的基礎上,設計和改進了規劃裝配序列遺傳算法,通過加入基礎件后的改進算法,獲得了更貼近實際裝配過程的產品裝配序列。該算法對初始裝配序列無特殊要求,初始種群加入由DELMIA軟件虛擬拆卸得到的可行裝配序列,由于這些裝配序列帶有經驗知識成份,其能有效地改善裝配序列種群的組成成份,加快算法向最優解或近優解的收斂速度。通過實例證明,由該方法快速搜索到最優或近優裝配序列,能夠用于指導產品實際裝配過程。
核心關注:拓步ERP系統平臺是覆蓋了眾多的業務領域、行業應用,蘊涵了豐富的ERP管理思想,集成了ERP軟件業務管理理念,功能涉及供應鏈、成本、制造、CRM、HR等眾多業務領域的管理,全面涵蓋了企業關注ERP管理系統的核心領域,是眾多中小企業信息化建設首選的ERP管理軟件信賴品牌。
轉載請注明出處:拓步ERP資訊網http://www.guhuozai8.cn/
本文標題:基于遺傳算法的產品裝配序列規劃研究