1 引言
傳統客車車架大多采用鋼材，車身較重。近年來，為了減重，新能源客車開始大量使用鋁合金，而鋁合金之間的連接對整個車身骨架性能有重大影響。鋁合金焊接相對于鋼焊接難度大且容易發生變形，所以需要減少鋁合金焊接的使用。榫卯結構是一種最簡單、穩定的連接方式，使用兩塊材料在不需第三者材料的介入下實現牢固連接，將榫卯結構的設計思想運用于以鋁合金擠壓型材為桿梁件的客車車身骨架中，可以一定程度上保持結構的完整性，大大減少焊接、鉚接的使用，起到減少重量、提高連接強度的作用。王念等對電動中巴車榫卯結構骨架進行有限元分析表明榫卯連接方式滿足相關工況的結構剛度和強度要求。本文選取車身骨架上的榫卯結構進行厚度和形狀優化。
2 有限元模型的建立
2.1 模型簡介
選取圖1車身骨架中的榫卯結構進行優化，有限元模型如圖1右邊所示，梁上開孔，將柱插入孔中，孔周圍的焊接采用共節點的方式連接，梁上的筋板剛好壓到柱上，形成類似于家具、建筑中的榫卯結構。所有的殼單元原始厚度均為2，其中梁的尺寸為75mmX45mmX400mm，梁筋板間的距離為25mm;柱的尺寸為75mmX25mmX400mm，柱的筋板間的距離為45mm。
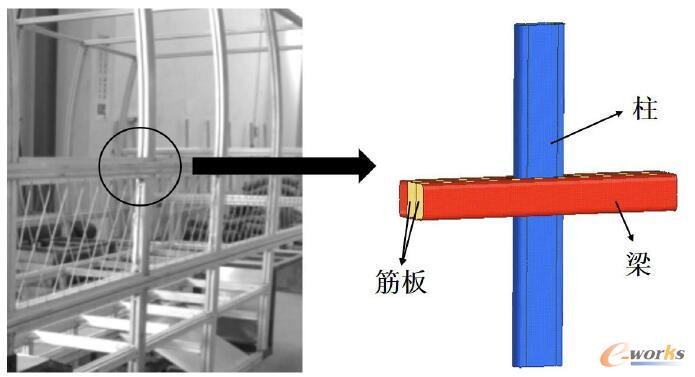
圖1 車身骨架圖和榫卯結構有限元模型
2.2 工況介紹
汽車的工況較為復雜，本模型提取5種典型工況進行分析，其中彎曲、緊急轉彎、緊急制動和扭轉4種工況使用OptiStruct求解，這4種工況的載荷和約束見圖2和表1;另1種工況求解汽車發生磕碰時結構在壓縮下的承載能力，使用RADIOSS進行求解，如圖3所示，底下為4個半徑為15mm的圓柱剛性墻，上面為一個半徑為50mm的球剛性墻壓頭，進行準靜態壓縮80mm，提取壓頭力-位移關系，力對位移積分求得結構吸收的能量，能量除以位移即平均載荷。
平均載荷定義為結構所吸收的能量除以對應的位移量s，平均載荷的定義公式為
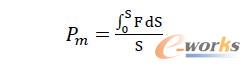
其主要衡量結構壓縮下的承載能力。
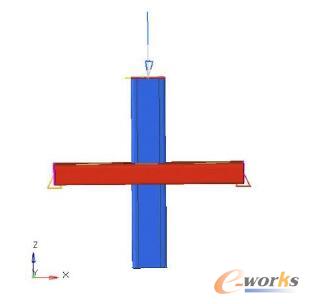
圖2 OptiStruct模型
表1 OptiStruct工況信息
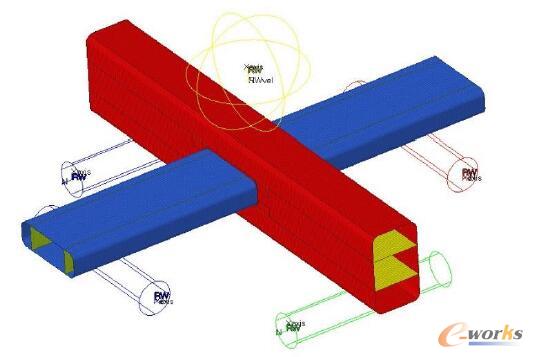
圖3 RADIOSS模型
3 HyperStudy優化模型的建立
優化設計三要素為設計變量、約束條件、目標函數。優化設計通常可以歸納為：在一定的約束條件下，選取設計變量，使目標函數達到最小（或最大），其數學表達式一般為：
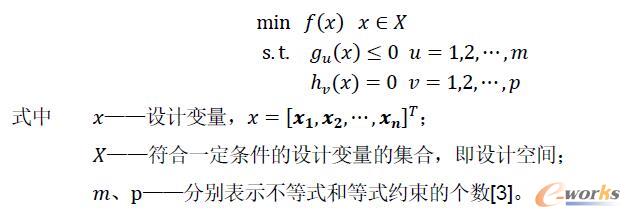
3.1 設計變量
本模型中要求梁和柱的筋板一樣厚、外框一樣厚，如圖4所示，黃色的為筋板，紅色的為外框。現以筋板的厚度、外框的厚度、柱的長和寬為設計變量，為了能夠優化柱的長和寬，需要先創建兩個shape，如圖5和圖6所示。
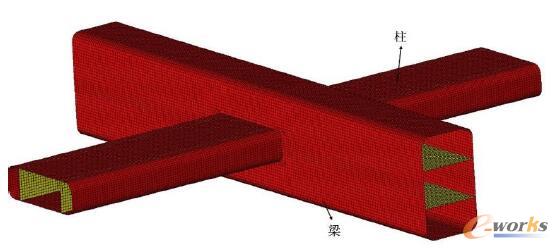
圖4 榫卯結構
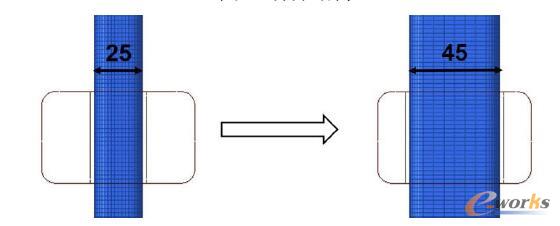
圖5 Shapel
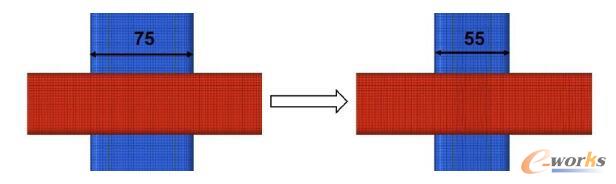
圖6 Shape2
設計變量的數學表達式如下
式中shape1,shape2為圖5和圖6對應的shape，th_jb為筋板的厚度，th_k為外框的厚度。
這4個變量在HyperStudy中的設置如圖7所示。其中變量5、6、7、8為RADIOSS模型的變量，把它們與OptiStruct模型的變量關聯。
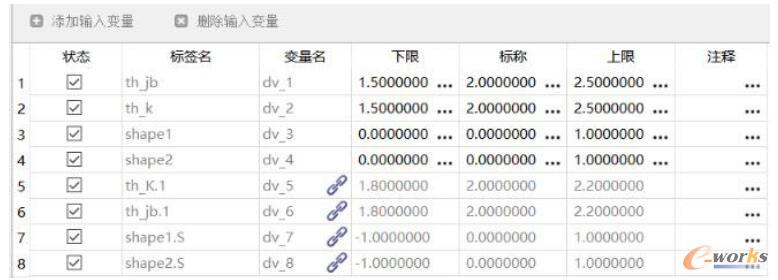
圖7 設計變量
3.2 約束條件
本優化是在保證靜剛度的前提下進行的，對于OptiStruct分析的彎曲、緊急轉彎、緊急制動和扭轉4種工況分別約束其最大位移，約束條件的數學表達式如下
式中disp_m、disp_s、disp_b和disp_t分別為彎曲工況、緊急轉彎工況、緊急制動工況和扭轉工況的最大位移。
約束條件在HyperStudy中的設置如圖8所示。
圖8 約束條件
3.3 目標函數
本優化為多目標優化，目標分別為最小質量和最大平均載荷。
其數學表達式如下
minmass
maxpm
式中mass為模型的質量，pm為平均載荷。從RADIOSS分析結果T01文件中得到接觸力、剛性球的位移與時間的關系，用integral求接觸力對位移的積分，其最大值除以位移即為平均載荷。
目標函數在HyperStudy中的設置如圖9所示。
圖9 目標設定
3.4 優化算法
HyperStudy包含非常豐富的優化算法，本案例為復雜的多目標優化問題，可以選擇的優化算法有全局自適應響應面法（GRSM)和多目標遺傳算法（MOGA)。由于多目標遺傳算法迭代次數過多，效率非常低，本優化問題選擇全局自適應響應面法。全局自適應響應面法在每一次迭代后，基于響應面的優化算法會產生新的計算樣本點，增加的樣本點會在局部搜索和全局搜索之間尋求一個較好的平衡。全局自適應響應面法在開始時利用少數的樣本點建立一個響應面并根據新的樣本點適應性地更新響應面以更好地擬合實際模型。全局自適應響應面法可以優化單目標和多目標的問題，具有全局搜索能力。
4 結果分析
經過50次迭代后得到的最優解如圖10所示。
圖10 最優解
在考慮輕量化的前提下選擇一個最優解，選擇一個比原來質量（0.0011341t）小的點（0.0010557，47930.906），對應的設計變量th_jb=1.5001550,th_k=1.9883701,shape1=0.5589178,shape2=0.9901122。把設計變量圓整后取th_jb=1.50,th_k=2.00,shape1=0.55,shape2=1.00。圓整后的模型如圖11所示，筋板厚為1.5mm，外框厚為2mm,其中梁的尺寸為75mm×45mm×400mm，梁筋板間的距離為36mm；柱的尺寸為55mm×36mm×400mm，柱的筋板間的距離為25mm。原模型的質量為1.1341kg，平均載荷為38578.7N;優化后的模型質量為1.0583kg，平均載荷為48212.2N。
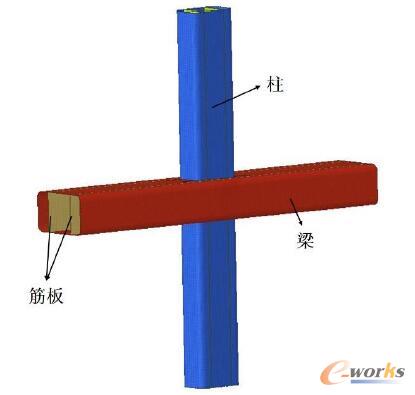
圖11 優化后圓整的模型
使用HyperGraph提取優化前后模型壓頭接觸力的力-位移曲線如圖12所示。
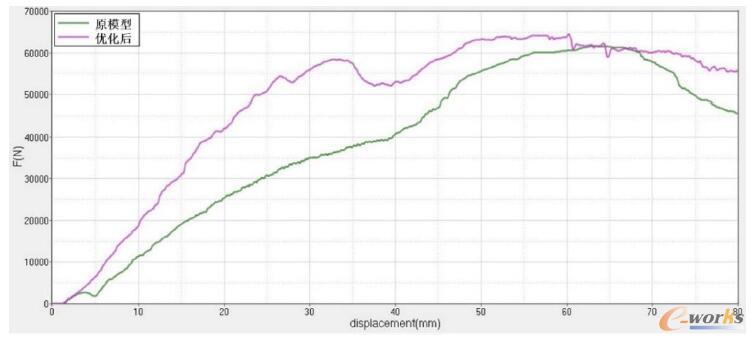
圖12 壓頭接觸力的力-位移曲線
優化前后的模型向下壓80mm后的結果如圖13所示，柱均出現了斷裂。
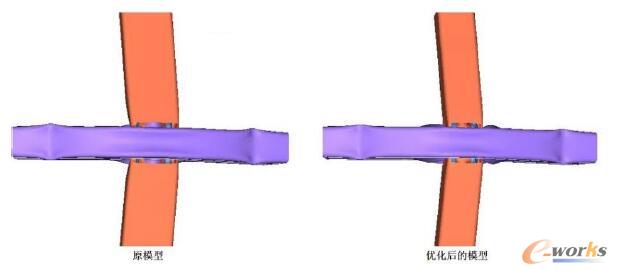
圖13 準靜態壓縮后的結果
5 結論
本文基于HyperStudy多學科優化平臺，以OptiStruct和RADIOSS為求解器對榫卯結構進行了厚度和形狀優化。通過優化設計，榫卯結構的壓縮承載能力得到明顯改善，平均載荷由38578.7N優化到48212.2N，增加了25.0%；質量從最原始的1.1341kg到優化后的1.0583kg，減重了6.7%。本研究在滿足靜剛度的要求下有效地實現了提高壓縮承載能力和輕量化，對機械設計的優化具有指導意義。
核心關注：拓步ERP系統平臺是覆蓋了眾多的業務領域、行業應用，蘊涵了豐富的ERP管理思想，集成了ERP軟件業務管理理念，功能涉及供應鏈、成本、制造、CRM、HR等眾多業務領域的管理，全面涵蓋了企業關注ERP管理系統的核心領域，是眾多中小企業信息化建設首選的ERP管理軟件信賴品牌。
轉載請注明出處：拓步ERP資訊網http://www.guhuozai8.cn/
本文網址：http://www.guhuozai8.cn/html/solutions/14019324615.html
相關文章
